در تحلیل مدارهای الکتریکی با اصطلاحاتی مانند امپدانس، مقاومت یا رزیستانس، راکتانس، ادمیتانس، ظرفیت یا کاپاسیتانس، اندوکتانس، رسانایی یا کندوکتانس، سوسپتانس و الاستانس سروکار خواهیم داشت.. اما به ظاهر عجیب یا ترسناک هستند و برخی از این واژهها کاربرد بیشتری در زمینه فعالیت ما دارند و با آموختن هدفمند آنها شیرینی به کار باز میگردد.. در مدارهای مغناطیسی نیز اصطلاحاتی مانند رلوکتانس و پرمانس وجود دارد.. اگر توجیه کاربرد و هدایت صحیح و البته انتقال بهتری در تحصیلات (مخصوصا دولتی) بود زندگی شیرینتر و آدمها با کارشان مرتبطتر و کارامدتر و شهر هم گل و بلبل میشد.
در صورتی که علاقمند به تحلیل مدارهای میکروشیپ یا طراحی مدارهای مورد علاقه خود هستید میتوانید از این پارامترها استفاده کنید..
بار الکتریکی (Q)
الکتریسیته همان حرکت الکترونها است. روشن شدن لامپها و کار کردن گوشیهای تلفن و تمامی تجهیزات برقی همه نتیجه حرکت الکترونها و انجام یک کار است.. الکترونها تحت تاثیر پتانسیل الکتریکی به حرکت در میایند.برای نشان دادن بار یا الکتریسیته از علامت e یا Q استفاده میشود. در سامانهٔ بینالمللی یکاها (SI) واحد بار الکتریکی کولن معادل بار الکتریکی ۱۰۱۸ × ۶٫۲۴۲ عدد پروتون یا بهطور ضرب شده به ۱ منفی (۱-) برابر با بار الکتریکی ۱۰۱۸ × ۶٫۲۴۲ عدد الکترون است؛ بنابراین بار یک الکترون e = 1.602 * 10-19 C کولن است. هر کولن، مقدار بار الکتریکی گذرنده در یک ثانیه و در جریان ثابت یک آمپر است. (1C = 1A . 1s)
مرتبط : نیمههادی! قسمت اول , جهت واقعی جریان الکتریکی , قانون اهم (روابط پرکاربرد مقاومت و پتانسیل و جریان الکتریکی) , بار الکتریکی
جریان (I)
میزان عبور الکترونها از یک نقطه مدار را جریان الکتریکی میگویند. واحد اندازه گیری جریان الکتریکی، آمپر است. یک آمپر جا به جایی ۱۸^۱۰ * ۶.۲۴۱ الکترون (یک کولمب) در یک ثانیه، از یک نقطه از مدار میباشد. در مدارات الکتریکی جریان الکتریکی را با واحد آمپر (A) و نماد I نمایش میدهند. مقاومت الکتریکی به عنوان کاهنده جریان یک شی روی میزان عبور الکترونها تاثیر دارد.
توضیح بیشتر : Electric Current
ولتاژ (V)
ولتاژ، که به آن نیروی الکترومغناطیسی نیز میگویند، اختلاف پتانسیل بار الکتریکی بین دو نقطه از میدان الکتریکی میباشد. واحد اندازهگیری ولتاژ، ولت است. در مدارات و شماتیکها و فرمول ها، ولتاژ با حرف (V) نمایش داده میشود.
در واقع ولتاژ، یک فشار الکتریکی ناشی از منبع مدار الکتریکی است که الکترونها را از طریق یک حلقه رسانا هدایت میکند و آنها را قادر به کارهایی مانند روشنایی میکند.
رزیستانس یا مقاومت (R)
رزیستانس (Resistance) درواقع همان مقاومت اهمی (رزیستور یا مقاومت عادی ساختار ماده) است. واحد اندازهگیری استاندارد مقاومت اهم Ω (نماد بزرگ یونانی نماد امگا) است و سمبل مقاومت در مدار با حرف R بزرگ نشان داده میشود و یک مقدار حقیقی دارد. از مقاومت برای کاهش عبور جریان (الکترونهای آزاد) ، تنظیم سطح سیگنالها، تقسیم ولتاژ، یا موارد بسیار دیگری استفاده میشود. هنگامی که جریان الکتریکی از یک مقاومت عبور میکند اختلاف ولتاژی بر اساس قانون اهم بین پایههای آن ایجاد میشود.
مقاومت برای عنصر پسیو مقاومت، در هر دو جریان الکتریکی DC و AC وجود داشته و مقدار آن در هر دو جریان یکسان است.
مقاومت، مشابه امپدانس، با اعمال ولتاژ، با عبور جریان مخالفت میکند.
یک امپدانس مقاومتی خالص، مؤلفه راکتیو امپدانس (سلفی یا خازنی) ندارد (مانند المنت هیتر، رادیاتور و یا مقاومت).
امپدانس مقاومت برابر با خود مقاومت است.
مرتبط : قانون اهم
امپدانس (Z)
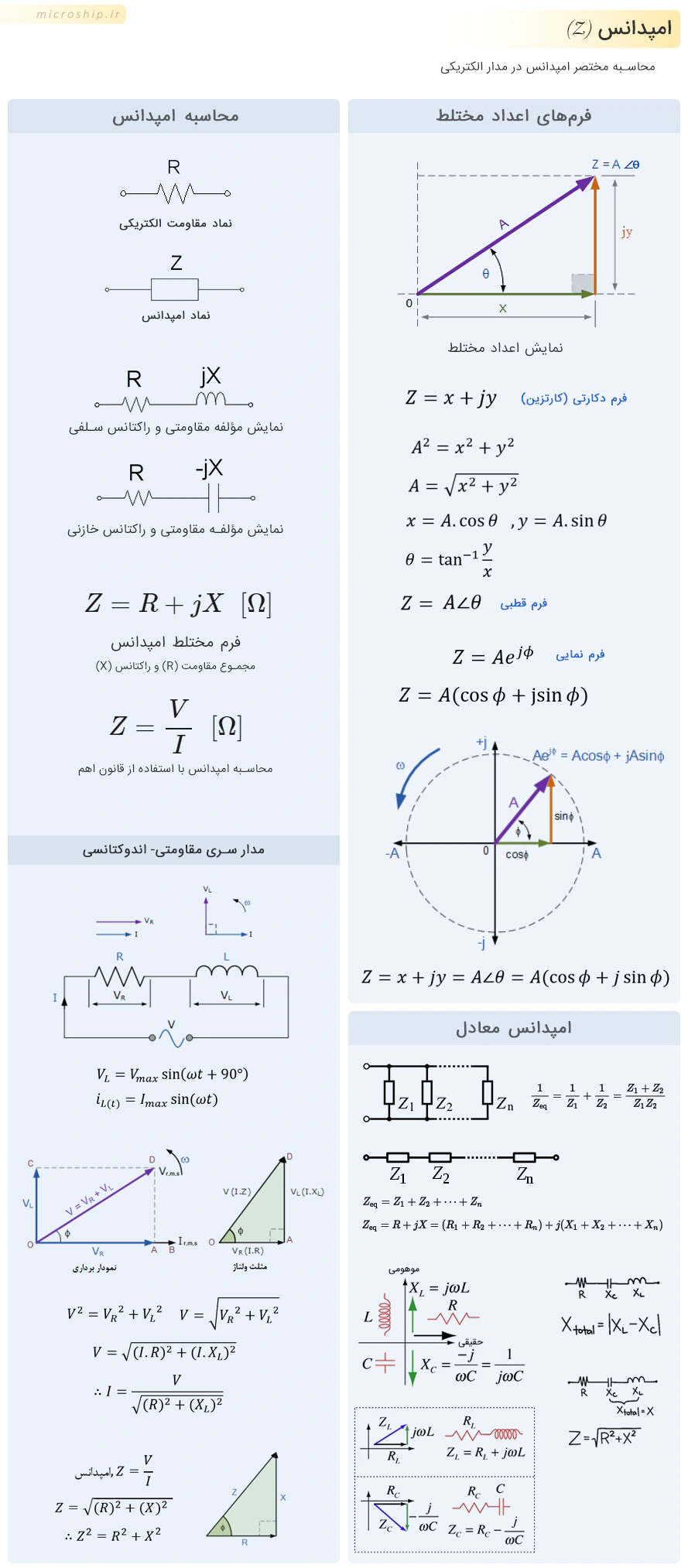
امپدانس یک حالت فازوری است و این پارامتر به صورت عدد مختلط (دارای مؤلفه حقیقی و موهومی) نمایش داده میشود و ممکن است متشکل از حالت اندوکتانسی، رزیستانسی، کاپاسیتانسی یا مجموع رزیستانسی و دوتای دیگر باشد. Z=R+JX
امپدانس، مخالفت کلی در برابر شارش یا عبور الکترونها (جریان الکتریکی) در یک مدار الکتریکی است. نماد امپدانس را با حرف بزرگ Z نمایش میدهند و واحد آن، اُهم (Ω) است.
امپدانس مجموع دو عامل کندکننده جریان شامل مقاومت (R) و راکتانس (X) است. مقاومت مؤلفه حقیقی امپدانس یا Re{Z} و راکتانس مؤلفه موهومی آن یا Im{Z} است. مؤلفه موهومی امپدانس، با حضور عناصری مانند سلف و خازن در مدار وجود دارد.
امپدانس میتواند با فرم مختلطی شامل بخش حقیقی و بخش موهومی نشان داده شود (که نتیجهی دو یا چند فازور است) به طوری که شکل تعمیم یافته آن به صورت Z=R+jX [Ω] است از قرار
Z : یک عدد مختلط
x : بخش حقیقی یا جز فعال
y : بخش موهومی یا جز انفعالی
j : توسط √-1 تعریف میشود..
برای تمایز یک عدد موهومی از یک عدد حقیقی، از حرف انگلیسی “j” که معمولا در مهندسی برق به عنوان عملگر “j “ معروف است، استفاده میشود. بنابراین، حرف “j” در مقابل یک عدد حقیقی قرار میگیرد تا نشاندهندهی عملکرد یک عدد موهومی باشد.
با ضرب j در راکتانس، امپدانس قطعه بدست میآید. +j به معنای این است که فاز ولتاژ 90درجه از جریان جلوتر است (در سلف).
j = 1∠+90° & -j = 1∠-90°
در ”فرم دکارتی“، یک عدد مختلط را میتوان، به عنوان یک نقطه در یک صفحه مختلط یا s نشان داد. بنابراین به عنوان مثال Z=6+j4، یک نقطه واحد را نشان میدهد؛ که مختصات آن، 6 را در محور حقیقی افقی و 4 را در محور موهومی عمودی، نشان میدهد.
برخلاف ”فرم دکارتی“ که نقاط را در صفحهی مختلط، رسم میکند؛ ”فرم قطبی“ عدد مختلط، با اندازه و زاویه نوشته میشود. بنابراین، یک بردار فرم قطبی به این صورت ارائه میشود: در جاییکه، Z عدد مختلط به شکلقطبی است، A اندازه یا مدول برداری است و Φ زاویه یا آرگومان A بوده که میتواند مثبت یا منفی باشد. اندازه و زاویه نقطه، همچنان به همان فرم مستطیل شکل باقی مانده اما اینبار محل نقطه به صورت قطبی به ”فرم مثلثی“ به صورت Z=A∠Φ نوشته میشود.روش سومی برای نمایش یک عدد مختلط، وجود دارد به نام ”فرم نمایی“ که شبیه فرم قطبی است که با طول (بزرگی) و زاویه فاز موج سینوسی مطابقت دارد اما از پایه لگاریتم طبیعی …e = 2.718 281 برای یافتن مقدار عدد مختلط استفاده مینماید.
فرم نمایی (که اویلر نامگذاری شده) برای یافتن موقعیت نقطه به صورت AejΦ ارائه میشود.
با پدید آمدن نمودار برداری و مثلث ولتاژ عناصر مدار (با تاثیر اختلاف فاز) و به تبع آن پدید آمدن مثلث مقاومت و راکتانس با دو ضلع یک مثلث زاویهدار قائمه در مدار مختلط RLC سری ، وتر مثلث یا امپدانس مدار را میتوان با قضیه فیثاغورث یافت به این صورت :Z2 = (R2 + X2) => Z = √(R2 + X2)
محاسبه امپدانس، کار دشواری نیست. جهت محاسبه امپدانس کل یک مدار، باید مقاومت کل (معادل) تمامی عناصر مقاومتی و راکتانس کل (معادل) تمامی عناصر پسیو سلف و خازن را بدانیم. نهایتا با امپدانس الکتریکی میتوان مانند یک مقاومت برخورد کرد.. یعنی در اتصال (ترکیب) سری، امپدانسها با هم جمع میشوند و در ترکیبهای موازی، امپدانس کل برابر است با معکوس مجموع ادمیتانسها (به معکوس امپدانس، ادمیتانس گفته میشود)
نکتهای در نظر بگیرید اگر دو عنصر سلف و خازن به صورت سری قرار گرفته باشند، راکتانس معادل آنها به صورت Xtotal = |XL - XC| محاسبه میشود. در مطلب معادل سنجی مدارهای ترکیبی R,L,C کاملتر در این مورد توضیح داده شده است.
(به دلیل تفاوت فاز در جریان و ولتاژ سلف و خازن در جریانهای متناوب، نمیتوان راکتانسها را با یکدیگر جمع کرد. در واقع راکتانسهای خازنی و سلفی هر کدام در زمانهای متفاوتی به حداکثر مقدار خود میرسند)
با استفاده از قانون اهم، امپدانس برای یک عنصر در مدار به این صورت بدست میآید: Z = V/I = [Ω]
جریان در یک مقاومت، یک خازن و یک سلف در حالت سری با منبع برق متناوب (AC) متفاوت است.
به عنوان مثال در مداری با ۳ عنصر پسیو خازن (Capacitor)، سلف (Icanductor) و مقاومت (Resistor) در جریان متناوب، با سه مقاومت متفاوت، به نامهای راکتانس خازنی (XC)، راکتانس سلفی (XL) و مقاومت عادی (R) روبهرو هستیم.
واژه «امپدانس» (Impedance) به مقاومتی که یک عنصر یا مدار به هنگام عبور جریان متناوب از خود نشان میدهد، اشاره دارد. در واقع امپدانس واژهای کلیتر از مقاومت بوده و در یک مدار به مجموع راکتانس خازنی و سلفی و مقاومت R، امپدانس گفته میشود.
مرتبط : معادل سنجی در مدارهای ترکیبی مقاومت ، خازن ، سلف ، Inductive Reactance ، Calculate Impedance
مرتبط : Electrical impedance , Impedance VS Resistance , Impedance and Complex Impedance
ادمیتانس (Y)
ادمیتانس، معکوس امپدانس است و میزان سهولت در عبور جریان را در اثر اعمال ولتاژ نشان میدهد. ادمیتانس را با حرف بزرگ Y نشان میدهند و واحد آن، زیمنس (S) است. این پارامتر، در حالت کلی یک عدد مختلط است و بهفرم زیر نوشته میشود:
Y=G+jB [S]
که مجموع کندوکتانس (رسانایی با نماد G) و سوسپتانس (B) است.
رسانایی، مؤلفه حقیقی ادمیتانس (Re{Y}) و سوسپتانس مؤلفه موهومی آن (Im{Y}) است. ادمیتانس را میتوان با عکس کردن امپدانس محاسله کرد: Y=1/Z [S]
قانون اهم برحسب ادمیتانس، ولتاژ و جریان بهصورتهای زیر بیان میشود:
V=I/Y [V] & I=VY [A]
توضیح بیشتر : Admittance
کندوکتانس (رسانایی) (G)
مفهوم رسانایی یا کندوکتانس، در برابر مقاومت قرار میگیرد و مؤلفه حقیقی ادمیتانس (Re [Y]) است و به همین دلیل، یک عدد مختلط نیست. رسانایی را با حرف بزرگ G نشان میدهند و واحد بین المللی (SI) آن، زیمنس (S) است. (واحد قدیمی آن مُهُو mho بود)
اگر امپدانس مؤلفه موهومی نداشته باشد و مقاومت خالص داشته باشیم، رسانایی را میتوان از روی معکوس مقاومت بهدست آورد:
G=1/R [S]
توضیح بیشتر : Electrical resistance and conductance
سوسِپتانس (B)
سوسپتانس، از نظر مفهومی در مقابل راکتانس قرار میگیرد و مؤلفه موهومی ادمیتانس ({Im{Y) است. سوسپتانس را با حرف بزرگ B نشان میدهند و واحد آن، زیمنس (S) است. (واحد قدیمی آن مُهُو mho بود)
اگر امپدانس، موهومی خالص باشد و مؤلفه حقیقی نداشته باشیم، سوسپتانس را میتوان با معکوس کردن راکتانس بهدست آورد:
B=1/X [S]
سوسپتانس، میزان سهولت در تغییر جریان یا ولتاژ مدار را نشان میدهد.
توضیح بیشتر : Susceptance
اندوکتانس (L)
اَندوکتانس (ضریب خودالقایی) همان حالت سلفی است که در پیچهها، ترانسفورماتورها و ماشینهای القایی پرکاربرد هستند. واحد اندازهگیری آن هانری (H) است و با سمبل L نشان داده میشوند. رابطه اندوکتانس: L = (µ×N ² ×A) / l
توضیح بیشتر : Inductance
راکتانس (X)
راکتانس (Reactance) را با حرف X بزرگ نشان میدهند و برابر با مؤلفه موهومی امپدانس ({Z} Re) است. بنابراین، مقدار راکتانس، یک عدد موهومی، و واحد آن اهم (Ω) است. (درواقع راکتانس حالت فازوری اندوکتانس و کاپاسیتانس است)
راکتانس مقاومت واکنشی شکل گرفته از میدانهای الکتریکی و مغناطیسی پدید آمده در عناصر پسیو خازن و سلف به هنگام عبور جریان الکتریکی متناوب (AC) است (که در برابر تغییر جهت جریان مخالفت می کند)، بنابراین در جریانهای الکتریکی ثابت (DC) عموماً پارامتر راکتانس تعریف نمیشود.
در فرکانسهای زیاد، امپدانس سلف زیاد است (سلف مانند مدار باز عمل میکند) و امپدانس خازن به سمت صفر میل میکند (خازن مانند اتصال کوتاه عمل میکند).. در فرکانسهای کم این موضوع برعکس میشود. (در برخورد با امپدانس مانند مقاومت رفتار میکنیم)
راکتانس، بسته به اینکه با تغییر ولتاژ یا جریان مخالفت کند، دو نوع دارد :
راکتانس سلفی (XL) / اندوکتانس (L)
در راکتانس سلفی یا القایی (XL) میدان مغناطیسی تولید شده مطابق با قانون لنز، عامل مخالفت در برابر تغییر جریان الکتریکی المان است.
راکتانس سلفی، به صورت حاصلضرب سرعت زاویهای و اندوکتانس جسم مورد نظر محاسبه میشود :
XL = ωL [Ω]
ω = 2πf [rad/sec]
که در آن، اندوکتانس بر حسب هانری (H) بیان میشود. فرکانس زاویهای ω برحسب رادیان بر ثانیه است و با ضرب 2π در فرکانس بهدست میآید. واحد اندازهگیری راکتانس سلفی اهم [Ω] است.
راکتانس سلفی، همیشه یک مؤلفه موهومی مثبت یا jX+ از امپدانس است :
Z = jXL
در یک مدار، راکتانس سلفی را معمولاً با یک سیمپیچ نشان میدهند، زیرا سلفها معمولاً از پیچاندن یک هادی (سیم) دور یک چنبره ساخته میشوند. راکتانس سلفی، از طریق تولید شار مغناطیسی، با عبور جریان مخالفت میکند. یک مثال خوب برای راکتانس سلفی، سیمپیچ ایدهآل مانند سیمپیچی در استاتور یک موتور یا ژنراتور است.
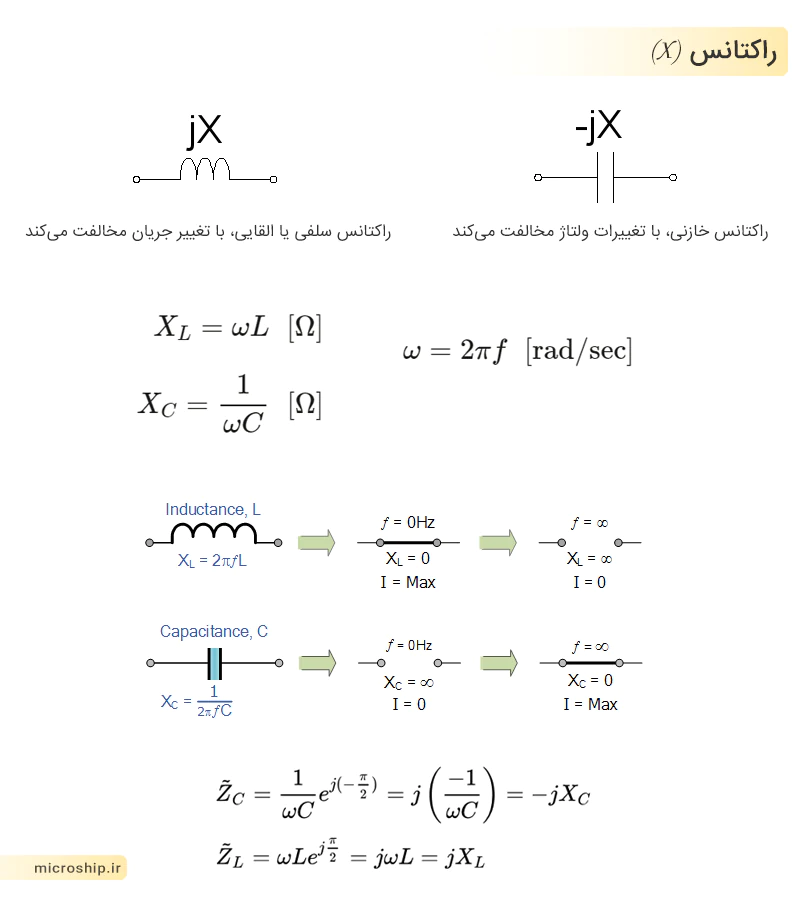
راکتانس خازنی (XC) / ظرفیت (C)
راکتانس خازنی یک مؤلفه امپدانس موهومی است که در برابر تغییرات ولتاژ المان، مقاومت میکند. واحد اندازهگیری راکتانس خازنی اهم [Ω] است.
راکتانس خازنی (XC) ناشی از مخالف بودن جهت میدان الکتریکی بین صفحات خازن با جهت جریان است.
خازن در یک جریان الکتریکی متناوب (AC) به طور مدام با عوض شدن جهت جریان، شارژ و دشارژ میشود. در واقع به هنگام شارژ جهت جریان عوض شده و بارهای قبلی که در راستای شارژ شدن در صفحات خازن جمع شده بودند (میدان حاصل از آنها) در برابر دشارژ شدن مقاومت میکنند. هر چه سرعت تغییر جهت جریان (فرکانس) بیشتر باشد، میزان راکتانس خازنی کاهش مییابد، چرا که میتوان گفت بار کمتری به هنگام شارژ در صفحات ذخیره میشود.
راکتانس خازنی، برابر با معکوس حاصلضرب فرکانس زاویهای و ظرفیت جسم مورد نظر است :
XC = 1/ωC = [Ω] & ω = 2πf [rad/sec] => XC = 1/2πfC [Ω]
که در آن، ظرفیت خازن برحسب فاراد (F) اندازهگیری میشود و فرکانس زاویهای ω برحسب رادیان بر ثانیه است و با ضرب 2π در فرکانس (HZ) بهدست میآید.
راکتانس خازنی، در مقابل ولتاژ ناشی از بارهای بین دو صفحه هادی مقاومت میکند. این پارامتر، همیشه یک مؤلفه موهومی یا jX- از امپدانس است :
Z = -jXC
در نمودار مدارها، معمولاً راکتانس خازنی را با نماد خازن نشان میدهند، زیرا معمولاً خازنها از دو صفحه هادی مجزا تشکیل میشوند که با یک دیالکتریک جدا شدهاند. یک مثال از راکتانس خازنی خالص، خازن ایدهآل کامل است.
توضیح بیشتر : Electrical Reactance
کاپاسیتانس (C)
کاپاسیتانس توانایی یک قطعه یا مدار برای جمع آوری و ذخیره انرژی در قالب یک بار الکتریکی است.
کاپاسیتانس (ظرفیت خازنی) همان حالت خازنی است که در خطوط انتقال بلند، مخصوصا خطوط بلند بدون بار کار برد دارند و موجب افزایش ولتاژ ناخواسته میشوند. واحد اندازه گیری آن فاراد F است و با سمبل C نشان داده میشود.
خازنها لوازم ذخیره کننده انرژی در اندازهها و شکلهای مختلف بوده که شامل دو صفحه رسانا (معمولا از جنس یک فلز نازک) هستند که بین یک عایق از جنس سرامیک، فیلم، شیشه یا مواد دیگر، حتی هوا قرار گرفتهاند.
توضیح بیشتر : Capacitance
الاستانس (S)
الاستانس با نماد S ، معکوس ظرفیت و واحد آن «فارادمعکوس» (F−1) است (فارادمعکوس، گاهی داراف (Daraf) نیز نامیده میشود). اصطلاح الاستانس بهندرت مورد استفاده قرار میگیرد.
توضیح بیشتر : Elastance
رِلوکتانس (R)
نیروی محرکه مغناطیسی، به شار مغناطیسی کل
رِلوکتانس مقاومت مغناطیسی یا به عبارتی نفوذ پذیری مغناطیسی است. این پارامتر از لحاظ ریاضی مشابه با مقاومت الکتریکی در مدارهای الکتریکی است.
R = F/Φ
رِلوکتانس (R) یا مقاومت مغناطیسی، کمیتی است که در مدارهای مغناطیسی، میزان مخالفت مدار را در برابر عبور شار مغناطیسی نشان میدهد. رلوکتانس معادل مدار مغناطیسی برابر با نسبت نیروی محرکه مغناطیسی (Phi) به شار مغناطیسی آن است.
توضیح بیشتر : Magnetic Reluctance
پِرمِآنس (P)
معکوس رلوکتانس را پِرمِانس (P) یا هدایت مغناطیسی مینامند که نشاندهنده میزان سهولت عبور شار است.
P = 1/R
توضیح بیشتر : Permeance
جمعبندی
خلاصه پارامترها و واحدهای آنها
| پارامتر | واحد | ||||
|---|---|---|---|---|---|
| فارسی | انگلیسی | نماد | فارسی | انگلیسی | نماد |
| امپدانس | Impedance | Z | اهم | Ohm | Ω |
| مقاومت یا رزیستانس | Resistance | R | اهم | Ohm | Ω |
| راکتانس | Reactance | X | اهم | Ohm | Ω |
| راکتانس سلفی | Inductive Reactance | XL | اهم | Ohm | Ω |
| اندوکتانس | Inductance | L | هانری | Henry | H |
| راکتانس خازنی | Capacitive Reactance | XC | اهم | Ohm | Ω |
| ظرفیت یا کاپاسیتانس | Capacitance | C | فاراد | Farad | F |
| ادمیتانس | Admittance | Y | زیمنس یا مهو | Siemens or Mho | S یا ℧ |
| رسانایی یا کندوکتانس | Conductance | G | زیمنس یا مهو | Siemens or Mho | S یا ℧ |
| سوسپتانس | Susceptance | B | زیمنس یا مهو | Siemens or Mho | S یا ℧ |
| الاستانس | Elastance | S | فاراد معکوس | Inverse Farad | F−1 |
| رلوکتانس | Reluctance | R | هانری معکوس | Inverse Henry | H−1 |
| پرمانس | Permeance | P | هانری | Henry | H |
منابع در متن لینک داده شده است..
دیگر : Electrical measurements , SI electromagnetism units , Difference between resistance and reactance and impedance , Inductive Reactance , Capacitive Reactance
برگرفته از: معرفی مختصر و مفید پارامترهای رایج الکتریکی + منابع (امتحانی)
برگرفته از: معرفی مختصر و مفید پارامترهای رایج الکتریکی + منابع (امتحانی)


